Beta wavelet
Continuous wavelets of compact support can be built [1], which are related to the beta distribution. The process is derived from probability distributions using blur derivative. These new wavelets have just one cycle, so they are termed unicycle wavelets. They can be viewed as a soft variety of Haar wavelets whose shape is fine-tuned by two parameters  and
and  . Closed-form expressions for beta wavelets and scale functions as well as their spectra are derived. Their importance is due to the Central Limit Theorem by Gnedenko&Kolmogorov applied for compactly supported signals [2].
. Closed-form expressions for beta wavelets and scale functions as well as their spectra are derived. Their importance is due to the Central Limit Theorem by Gnedenko&Kolmogorov applied for compactly supported signals [2].
Contents |
Beta distribution
The beta distribution is a continuous probability distribution defined over the interval 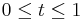 . It is characterised by a couple of parameters, namely
. It is characterised by a couple of parameters, namely  and
and  according to:
according to:
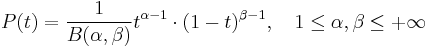 .
.
The normalising factor is 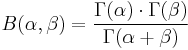 ,
,
where 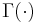 is the generalised factorial function of Euler and
is the generalised factorial function of Euler and 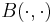 is the Beta function [4].
is the Beta function [4].
Gnedenko-Kolmogorov central limit theorem revisited
Let 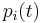 be a probability density of the random variable
be a probability density of the random variable 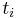 ,
, 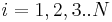 i.e.
i.e.
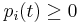 ,
, 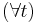 and
and 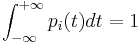 .
.
Suppose that all variables are independent.
The mean and the variance of a given random variable 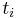 are, respectively
are, respectively
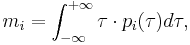
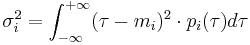 .
.
The mean and variance of  are therefore
are therefore 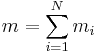 and
and 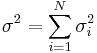 .
.
The density 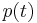 of the random variable corresponding to the sum
of the random variable corresponding to the sum 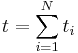 is given by the
is given by the
Central Limit Theorem for distributions of compact support (Gnedenko and Kolmogorov) [2].
Let 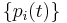 be distributions such that
be distributions such that 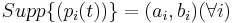 .
.
Let 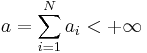 , and
, and 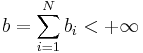 .
.
Without loss of generality assume that 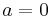 and
and 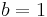 .
.
The random variable  holds, as
holds, as 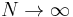 ,
, 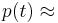
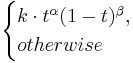
where 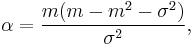 and
and 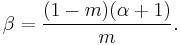
Beta wavelets
Since 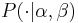 is unimodal, the wavelet generated by
is unimodal, the wavelet generated by
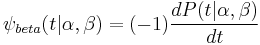 has only one-cycle (a negative half-cycle and a positive half-cycle).
has only one-cycle (a negative half-cycle and a positive half-cycle).
The main features of beta wavelets of parameters  and
and  are:
are:
![Supp(\psi )=[ \frac{-1}{\sqrt{{\beta }/ \alpha }}\sqrt{\alpha %2B \beta %2B1},\sqrt{ \frac{\beta }{\alpha }} \sqrt{\alpha %2B\beta %2B1}]=[a,b].](/2012-wikipedia_en_all_nopic_01_2012/I/0453072530f39e787484e5636d1913c7.png)
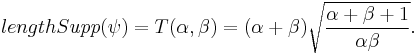
The parameter 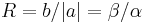 is referred to as “cyclic balance”, and is defined as the ratio between the lengths of the causal and non-causal piece of the wavelet. The instant of transition
is referred to as “cyclic balance”, and is defined as the ratio between the lengths of the causal and non-causal piece of the wavelet. The instant of transition 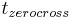 from the first to the second half cycle is given by
from the first to the second half cycle is given by
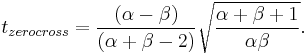
The (unimodal) scale function associated with the wavelets is given by
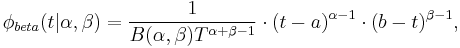
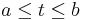 .
.
A closed-form expression for first-order beta wavelets can easily be derived. Within their support,
![\psi_{beta}(t|\alpha ,\beta ) =\frac{-1}{B(\alpha ,\beta )T^{\alpha %2B\beta -1}} \cdot [\frac{\alpha -1}{t-a}-\frac{\beta -1}{b-t}] \cdot(t-a)^{\alpha -1} \cdot(b-t)^{\beta -1}](/2012-wikipedia_en_all_nopic_01_2012/I/a745c6bb7069c3cb48b613a00ae0af51.png)
Beta wavelet spectrum
The beta wavelet spectrum can be derived in terms of the Kummer hypergeometric function [5].
Let 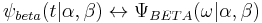 denote the Fourier transform pair associated with the wavelet.
denote the Fourier transform pair associated with the wavelet.
This spectrum is also denoted by 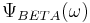 for short. It can be proved by applying properties of the Fourier transform that
for short. It can be proved by applying properties of the Fourier transform that
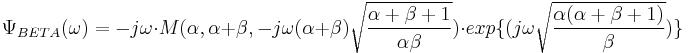
where 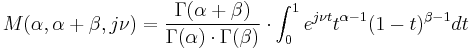 .
.
Only symmetrical  cases have zeroes in the spectrum. A few asymmetric
cases have zeroes in the spectrum. A few asymmetric 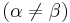 beta wavelets are shown in Fig. Inquisitively, they are parameter-symmetrical in the sense that they hold
beta wavelets are shown in Fig. Inquisitively, they are parameter-symmetrical in the sense that they hold 
Higher derivatives may also generate further beta wavelets. Higher order beta wavelets are defined by 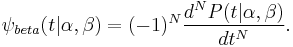
This is henceforth referred to as an  -order beta wavelet. They exist for order
-order beta wavelet. They exist for order 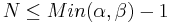 . After some algebraic handling, their closed-form expression can be found:
. After some algebraic handling, their closed-form expression can be found:
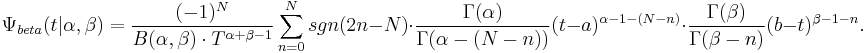
References
- [1] H.M. de Oliveira, G.A.A. Araújo, Compactly Supported One-cyclic Wavelets Derived from Beta Distributions, Journal of Communication and Information Systems, vol.20, n.3, pp.27-33, 2005.
- http://www.iecom.org.br/
- http://www2.ee.ufpe.br/codec/WEBLET.html
- http://www2.ee.ufpe.br/codec/beta.html
- [2] B.V. Gnedenko and A.N. Kolmogorov, Limit Distributions for Sums of Independent Random Variables, Reading, Ma: Addison-Wesley, 1954.
- [3] W.B. Davenport, Probability and Random Processes, McGraw-Hill /Kogakusha, Tokyo, 1970.
- [4] P.J. Davies, Gamma Function and Related Functions, in: M. Abramowitz; I. Segun (Eds.), Handbook of Mathematical Functions, New York: Dover, 1968.
- [5] L.J. Slater, Confluent Hypergeometric Function, in: M. Abramowitz; I. Segun (Eds.), Handbook of Mathematical Functions, New York: Dover, 1968.